MODELACIÓN: APLICACIÓN DE LA DERIVADA
Introducción
En el estudio del Cálculo Diferencial es primordial el concepto de variación o cambio continuo.
A través del uso del concepto de derivada se logra conocer algunas propiedades relevantes de las
funciones.
El estudio de estas características facilita la representación gráfica y la interpretación analítica
de las mismas, lo que posibilita su mejor entendimiento.
Muchos de los aspectos de la vida diaria como los de las ciencias y las ingenierías tienen que ver con el
cambio de las cosas y, en especial, con el cambio de una variable con relación a otras.
Las aplicaciones de la derivada en diversos campos pueden clasificarse en dos grupos:
a) La derivada como índice matemático
Expresa la tasa de variación o razón de cambio. En distintas disciplinas como Electricidad , Electrónica , Termodinámica , Mecánica , Economía , Biología , etc , resulta de importancia fundamental no sólo saber que determinada magnitud o cantidad varía respecto de otra , sino conocer cuán rápido se produce esa variación.
b) La derivada en Optimización de Funciones
Los problemas llamados de optimización, desde el punto de vista
matemático se reducen a problemas de determinación de máximos y mínimos
absolutos de funciones de una variable real en determinados intervalos.
A una empresa de transporte seguramente le interesa que el costo por kilómetro de
sus viajes sea el menor posible.
En Electrotecnia, interesará cómo diseñar determinado dispositivo para que su consumo
de energía sea mínimo.
Una empresa de construcción le interesará cómo dimensionar un silo
para grano para que el costo de la construcción sea el más bajo posible. Y a un vendedor
se interesará cuál es el precio de venta de su producto para obtener el mayor
beneficio posible.
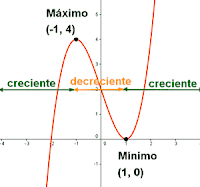
II.3.1. MÁXIMOS Y MÍNIMOS (EXTREMOS DE UNA FUNCIÓN)
El localizar valores extremos es el objetivo básico de la optimización matemática.
Cuando evaluamos una función f(x) se
localizan en la gráfica los puntos que describen el comportamiento de la
función, cuando se evalúa la derivada f’(x), los puntos que se obtienen
representa la pendiente de la recta en ese punto.
Se quiere calcular la pendiente de la recta
tangente (Toca en 1 solo punto) de la función f(x), en cualquier punto de ella
:
Como en cada punto de una curva f(x) existe una única recta tangente, entonces podemos pensar que para cada valor (x0,x1,x2,etc.) de este punto, la pendiente representa una "altura" para el mismo.
Es decir, podemos construir una nueva función representativa de éstas. Esta función se llamará Función Derivada f'(x).
En resumen : "De la pendiente de
una función f(x) (azul) se obtiene la altura de la grafica de la derivada f’(x) (rosa) “
Para comprender los puntos críticos: puntos de inflexión, máximos y mínimos es importante conocer las gráficas de las funciones polinomiales como se muestra en el video a continuación
